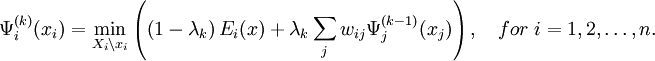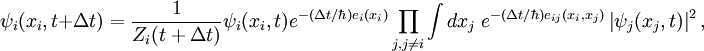协同优化算法_2_太古娱乐移民出国新闻站

协同优化算法_2

新闻资讯 | 2024-03-12 11:40

协同优化算法的原理是将一复杂的目标函数分解成简单的子目标函数，然后再将这些子目标函数进行协同优化。具体说来，协同优化是在优化每一子目标函数同时综合考虑其它子目标函数的结果，使子目标函数之间的优化结果能够一致。优化结果一致是指使每一变量的值在每一子目标函数的优化结果中能够一致。一般来说，可以证明，如果变量的值一致则为最优解。协同优化算法没有局部最优问题同时具有非常良好的收敛特性。它很好地解决了许多实际中非线性优化及组合优化难题。

如果目标函数是一n个变量的函数 $E(x_1, x_2, \ldots, x_n)$ ,简写成 $E(x)$ ,协同优化算法先将它分解成n个简单的子目标函数:

$E(x) = E_1(x) + E_2(x) + \ldots + E_n(x)$ .

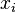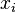如果单独优化每一子目标函数,则它们的结果很难达到一致。例如,变量 $x_i$ 在包含它的子目标函数中的最优解值很难相同。对于 $i=1,2,\ldots,n$ ,如果我们取 $E_i(x)$ 的最优解中 $x_i$ 的值作为该变量的值，表示成 $ilde{x}_i$ ,

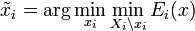$ilde{x}_i = \arg \min_{x_i} \min_{X_i \setminus x_i} E_i(x)$ ，这里， $X_i$ 是 $E_i(x)$ 的变量集， $X_i \setminus x_i$ 指变量集 $X_i$ 除去元素 $x_i$ ，

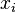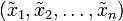$( ilde{x}_1, ilde{x}_2,\ldots, ilde{x}_n)$ 则很难为原目标函数 $E(x)$ 的最优解。

为了使子目标函数之间的优化结果能够一致，协同优化算法在优化每一子目标函数 $E_i(x)$ 同时考虑其它子目标函数的结果,

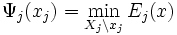$\Psi_j(x_j) = \min_{X_j \setminus x_j} E_j(x)$ 。

具体做法是利用其它子目标函数的优化结果通过数值加权修正每一个子目标函数如下,

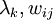$\left(1 - \lambda \right) E_i(x) + \lambda_k \sum_{j} w_{ij} \Psi_j(x_j)$ ，这里， $\lambda_k,w_{ij}$ 为加权系数，满足 $0 \le \lambda_k,w_{ij} \le 1$ 。

然后对修正后的子目标函数进行优化，优化结果再叠代放入修正的子目标函数中。协同优化算法的叠代方程如下,

$\Psi^{(k)}_i (x_i) = \min_{X_i \setminus{x_i}}\left( \left(1 - \lambda_k \right) E_i(x) +\lambda_k \sum_{j} w_{ij} \Psi^{(k-1)}_j(x_j)\right), \quad for \; i=1,2,\ldots,n.$

协同优化结果使每一变量的值在每一子目标函数的优化结果中达到一致。如果一致，则子目标函数的优化解既为最优解。

现代优化理论中最重要的未解难题是发现通用的全局最优化条件。由于没有全局最优化条件，我们不知道哪里可以找到最优解，也不知道现有解是不是最优解. 因此,我们不知道如何更有效地组织优化过程及何时及时中断搜索。任何全局最优化条件既有理论意义和实用价值。协同优化算法基于一种全新的优化原理解决了这一重要问题。

从协同优化算法可以推导出薛定谔方程。

假设目标能量函数为

$E(x_1, x_2, \ldots, x_n) = \sum^{n}_{i=1} \left(e_i (x_{i}) + \sum^{n}_{j:~j > i} e_{ij} (x_i, x_j) \right), \quad where \; e_{ij}(x_i, x_j) = e_{ji}(x_j, x_i).$

协同优化算法在半环 $(C,+, imes)$ 上的形式为

$\psi_i(x_i, t + \Delta t) = \frac{1}{Z_i (t + \Delta t)} \psi_i(x_i, t) e^{-(\Delta t/\hbar)e_i(x_i)} \prod_{j, j ot = i} \int d x_j \; e^{-(\Delta t/\hbar)e_{ij}(x_i, x_j)} \left|\psi_j (x_j, t)\right|^2,$

如果让 $\Delta t \rightarrow 0^{+}$ 及用高斯函数平滑 $\psi_i \left(x_i,t \right)$ ,则上式收敛后变成薛定谔方程如下:

$E_i \psi_i(x_i, t) = \left( -\frac{\hbar^2}{2 m_i} abla^2_i + V_i(x_i) \right) \psi_i(x_i, t);$

这里

$V_i(x_i) = e_i + \sum_{j, j ot = i} \int d x_j~e_{ij} |\psi_j (x_j, t)|^2.$

薛定谔方程是物理学中最基本的方程。因此，我们可以对自然界中一般分子及蛋白分子如何形成这一非线性优化问题从全局优化的角度有进一步更深的认识。

X. Huang, “Deriving the Normalized Min-Sum Algorithm from Cooperative Optimization”, accepted by IEEE Information Theory Workshop, Chengdu, China, 2006 (网上下载).

X. Huang, ``The cooperative optimization metaheuristic: Inspiration from nature and applications, Computational Intelligence, ICIC 2005, Springer-Verlag, LNAI 4114, 2006, pp. 1246--1251.

X. Huang, ``A general extension of constraint propagation for constraint optimization, Principles of Practice of Constraint Programming - CP 2004, Spinger-Verlag, LNCS 3258, 2004, pp. 737--741.

X. Huang, ``Near perfect decoding of LDPC codes, Proceedings of IEEE International Symposium on Information Theory (ISIT), 2005, pp. 302--306 (网上下载).

X. Huang, “A New Kind of Hopfield Networks for Finding Global Optimum”, International Joint Conference on Neural Networks, Montreal, Canada, 2005, pp.764-769 (网上下载).

X. Huang, ``Cooperative optimization for solving large scale combinatorial problems, Theory and Algorithms for Cooperative Systems, Series on Computers and Operations Research, World Scientific, 2004, pp. 117--156 (ISBN 981-256-020-3).

X. Huang, ``Image segmentation by cooperative optimization, IEEE International Conference on Image Processing (ICIP), Singapore, 2004, pp. 945--948.

X. Huang, ``Cooperative optimization for energy minimization in computer vision: A case study of stereo matching, Pattern Recognition, 26th DAGM Symposium, Springer-Verlag, LNCS 3175, 2004, pp. 302--309.

X. Huang, ``A general framework for constructing cooperative global optimization algorithms, Frontiers in Global Optimization, Nonconvex Optimization and Its Applications, Kluwer Academic Publishers, 2004, pp. 179--221 (ISBN 1-4020-7699-1).

X. Huang, “A Polynomial Time Algorithm for Solving NP-hard Problems in Practice”, ACM SIGACT Volume 34, Issue 1, March 2003, pp. 101-108.

X. Huang, “A Cooperative Search Approach for Global Optimization”, Oral Presentation at the First International Conference on Optimization Methods and Software, Hangzhou, China, 2002.

黄晓非,丁溯泉,杨知行,吴佑寿,"GF(q)域上的低密度校验(LDPC)码的译码及其在深空通讯中的应用",飞行器测控学报",第25卷,第2期,2006年4月.